ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA
Encontre a equação geral para parábola de vértice V(4, 2) e foco F(1, 2).
y2 - 6x + 2 + 22 = 0
y2 - 4x + 12y + 44 = 0
y2 - 4x – 12y - 48 = 0
y2 + 12x – 4y - 52 = 0
y2 + 12x – 4y - 44 = 0
Analise as afirmações feitas sobre a classificação dos pares de retas
r: 6x + 7y + 3 = 0 e s: 12x + 14y – 21 = 0,
e
t: x + 7y – 10 = 0 e v: - 7x + y – 3 = 0
A seguir assinale a alternativa correta.
r e s não são paralelas e v e t são perpendiculares.
r e s são paralelas e v e t não são perpendiculares.
r e s não são paralelas e v e t não são perpendiculares.
r e s são paralelas e v e t são concorrentes e não perpendiculares.
r e s são paralelas e v e t são perpendiculares.
Sistemas lineares é um conjunto de equações lineares, com m equações e n incógnitas. A solução de um sistema linear é a solução de todas as equações lineares.
A resolução de sistemas lineares tem aplicação nos mais diversos campos da ciência e da engenharia, como a eletrodinâmica, a eletrônica, a estática, a aerodinâmica, entre outras.
Sobre o sistema a seguir, é correto afirmar que:

x1 = - 3/4
x1 = - 4
x1 = x2
x1 = - 1/3
x1 = 9/4
Sejam X, Y e Z três artigos distintos que são vendidos em certa loja. Sabe-se que: X custa tanto quanto Y e Z juntos; o preço de Y é a diferença entre o dobro do de X e 50 reais; o preço de Z é a diferença entre o triplo do de Y e 80 reais. Nessas condições, pela compra dos três artigos, sendo um único exemplar de cada tipo, deverão ser desembolsados:
R$ 120, 00
R$ 100, 00
R$ 80, 00
R$ 150, 00
R$ 60, 00
Reduzir a equação x2 + y2 + z2 – 25 = 0 à forma canônica e identificar a superfície.





Considerando a equação da superfície expressa por
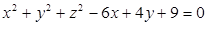
Assinale a alternativa correta.
Refere-se a uma superfície cilíndrica de centro de coordenadas (3, -2, 0) e raio igual a 4.
Refere-se a uma superfície cilíndrica de centro de coordenadas (3, 2, 0) e raio igual a 2.
Refere-se a uma superfície esférica de centro de coordenadas (3, 2, 0) e raio igual a 2.
Refere-se a uma superfície cônica de centro de coordenadas (-3, -2, 0) e raio igual a 4.
Refere-se a uma superfície esférica de centro de coordenadas (3, -2, 0) e raio igual a 2.
Dados os vetores u (-5,3,4) e v (2,1, 3). Assinale a alternativa que expressa o resultado do produto (3u + 2v) . (2u - v).
- 123
150
- 277
277
123
As coordenadas do centro e o raio das circunferências, cujas equações são
c1: (x – 5)2 + (y – 4)2 = 1 e c2: (x – 2)2 + y2 = 4, estão representadas na alternativa:
c1: Centro = (5, 4) e Raio =1 e c2: Centro = (2, 0 ) e Raio = 2
c1: Centro = (4, 5) e Raio =1 e c2: Centro = (2, 0 ) e Raio = 3
c1: Centro = (5, 0) e Raio = 2 e c2: Centro = (- 2, 4 ) e Raio =1
c1: Centro = (5, 4) e Raio = 1 e c2: Centro = (0, 2 ) e Raio = 2
c1: Centro = (5, - 4) e Raio = 2 e c2: Centro = (2, 0 ) e Raio = 2
Assinale a alternativa que representa a distância focal da hipérbole de equação 36x2 – 16y2 = 576.
y2 - 6x + 2 + 22 = 0
y2 - 4x + 12y + 44 = 0
y2 - 4x – 12y - 48 = 0
y2 + 12x – 4y - 52 = 0
y2 + 12x – 4y - 44 = 0
Analise as afirmações feitas sobre a classificação dos pares de retas
r: 6x + 7y + 3 = 0 e s: 12x + 14y – 21 = 0,
e
t: x + 7y – 10 = 0 e v: - 7x + y – 3 = 0
A seguir assinale a alternativa correta.
r e s não são paralelas e v e t são perpendiculares.
r e s são paralelas e v e t não são perpendiculares.
r e s não são paralelas e v e t não são perpendiculares.
r e s são paralelas e v e t são concorrentes e não perpendiculares.
r e s são paralelas e v e t são perpendiculares.
Sistemas lineares é um conjunto de equações lineares, com m equações e n incógnitas. A solução de um sistema linear é a solução de todas as equações lineares.
A resolução de sistemas lineares tem aplicação nos mais diversos campos da ciência e da engenharia, como a eletrodinâmica, a eletrônica, a estática, a aerodinâmica, entre outras.
Sobre o sistema a seguir, é correto afirmar que:

x1 = - 3/4
x1 = - 4
x1 = x2
x1 = - 1/3
x1 = 9/4
Sejam X, Y e Z três artigos distintos que são vendidos em certa loja. Sabe-se que: X custa tanto quanto Y e Z juntos; o preço de Y é a diferença entre o dobro do de X e 50 reais; o preço de Z é a diferença entre o triplo do de Y e 80 reais. Nessas condições, pela compra dos três artigos, sendo um único exemplar de cada tipo, deverão ser desembolsados:
R$ 120, 00
R$ 100, 00
R$ 80, 00
R$ 150, 00
R$ 60, 00
Reduzir a equação x2 + y2 + z2 – 25 = 0 à forma canônica e identificar a superfície.





Considerando a equação da superfície expressa por
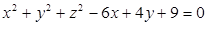
Assinale a alternativa correta.
Refere-se a uma superfície cilíndrica de centro de coordenadas (3, -2, 0) e raio igual a 4.
Refere-se a uma superfície cilíndrica de centro de coordenadas (3, 2, 0) e raio igual a 2.
Refere-se a uma superfície esférica de centro de coordenadas (3, 2, 0) e raio igual a 2.
Refere-se a uma superfície cônica de centro de coordenadas (-3, -2, 0) e raio igual a 4.
Refere-se a uma superfície esférica de centro de coordenadas (3, -2, 0) e raio igual a 2.
Dados os vetores u (-5,3,4) e v (2,1, 3). Assinale a alternativa que expressa o resultado do produto (3u + 2v) . (2u - v).
- 123
150
- 277
277
123
As coordenadas do centro e o raio das circunferências, cujas equações são
c1: (x – 5)2 + (y – 4)2 = 1 e c2: (x – 2)2 + y2 = 4, estão representadas na alternativa:
c1: Centro = (5, 4) e Raio =1 e c2: Centro = (2, 0 ) e Raio = 2
c1: Centro = (4, 5) e Raio =1 e c2: Centro = (2, 0 ) e Raio = 3
c1: Centro = (5, 0) e Raio = 2 e c2: Centro = (- 2, 4 ) e Raio =1
c1: Centro = (5, 4) e Raio = 1 e c2: Centro = (0, 2 ) e Raio = 2
c1: Centro = (5, - 4) e Raio = 2 e c2: Centro = (2, 0 ) e Raio = 2
Assinale a alternativa que representa a distância focal da hipérbole de equação 36x2 – 16y2 = 576.
r e s não são paralelas e v e t são perpendiculares.
r e s são paralelas e v e t não são perpendiculares.
r e s não são paralelas e v e t não são perpendiculares.
r e s são paralelas e v e t são concorrentes e não perpendiculares.
r e s são paralelas e v e t são perpendiculares.
Sistemas lineares é um conjunto de equações lineares, com m equações e n incógnitas. A solução de um sistema linear é a solução de todas as equações lineares.
A resolução de sistemas lineares tem aplicação nos mais diversos campos da ciência e da engenharia, como a eletrodinâmica, a eletrônica, a estática, a aerodinâmica, entre outras.
Sobre o sistema a seguir, é correto afirmar que:

x1 = - 3/4
x1 = - 4
x1 = x2
x1 = - 1/3
x1 = 9/4
Sejam X, Y e Z três artigos distintos que são vendidos em certa loja. Sabe-se que: X custa tanto quanto Y e Z juntos; o preço de Y é a diferença entre o dobro do de X e 50 reais; o preço de Z é a diferença entre o triplo do de Y e 80 reais. Nessas condições, pela compra dos três artigos, sendo um único exemplar de cada tipo, deverão ser desembolsados:
R$ 120, 00
R$ 100, 00
R$ 80, 00
R$ 150, 00
R$ 60, 00
Reduzir a equação x2 + y2 + z2 – 25 = 0 à forma canônica e identificar a superfície.





Considerando a equação da superfície expressa por
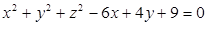
Assinale a alternativa correta.
Refere-se a uma superfície cilíndrica de centro de coordenadas (3, -2, 0) e raio igual a 4.
Refere-se a uma superfície cilíndrica de centro de coordenadas (3, 2, 0) e raio igual a 2.
Refere-se a uma superfície esférica de centro de coordenadas (3, 2, 0) e raio igual a 2.
Refere-se a uma superfície cônica de centro de coordenadas (-3, -2, 0) e raio igual a 4.
Refere-se a uma superfície esférica de centro de coordenadas (3, -2, 0) e raio igual a 2.
Dados os vetores u (-5,3,4) e v (2,1, 3). Assinale a alternativa que expressa o resultado do produto (3u + 2v) . (2u - v).
- 123
150
- 277
277
123
As coordenadas do centro e o raio das circunferências, cujas equações são
c1: (x – 5)2 + (y – 4)2 = 1 e c2: (x – 2)2 + y2 = 4, estão representadas na alternativa:
c1: Centro = (5, 4) e Raio =1 e c2: Centro = (2, 0 ) e Raio = 2
c1: Centro = (4, 5) e Raio =1 e c2: Centro = (2, 0 ) e Raio = 3
c1: Centro = (5, 0) e Raio = 2 e c2: Centro = (- 2, 4 ) e Raio =1
c1: Centro = (5, 4) e Raio = 1 e c2: Centro = (0, 2 ) e Raio = 2
c1: Centro = (5, - 4) e Raio = 2 e c2: Centro = (2, 0 ) e Raio = 2
Assinale a alternativa que representa a distância focal da hipérbole de equação 36x2 – 16y2 = 576.
x1 = - 3/4
x1 = - 4
x1 = x2
x1 = - 1/3
x1 = 9/4
Sejam X, Y e Z três artigos distintos que são vendidos em certa loja. Sabe-se que: X custa tanto quanto Y e Z juntos; o preço de Y é a diferença entre o dobro do de X e 50 reais; o preço de Z é a diferença entre o triplo do de Y e 80 reais. Nessas condições, pela compra dos três artigos, sendo um único exemplar de cada tipo, deverão ser desembolsados:
R$ 120, 00
R$ 100, 00
R$ 80, 00
R$ 150, 00
R$ 60, 00
Reduzir a equação x2 + y2 + z2 – 25 = 0 à forma canônica e identificar a superfície.





Considerando a equação da superfície expressa por
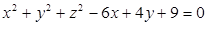
Assinale a alternativa correta.
Refere-se a uma superfície cilíndrica de centro de coordenadas (3, -2, 0) e raio igual a 4.
Refere-se a uma superfície cilíndrica de centro de coordenadas (3, 2, 0) e raio igual a 2.
Refere-se a uma superfície esférica de centro de coordenadas (3, 2, 0) e raio igual a 2.
Refere-se a uma superfície cônica de centro de coordenadas (-3, -2, 0) e raio igual a 4.
Refere-se a uma superfície esférica de centro de coordenadas (3, -2, 0) e raio igual a 2.
Dados os vetores u (-5,3,4) e v (2,1, 3). Assinale a alternativa que expressa o resultado do produto (3u + 2v) . (2u - v).
- 123
150
- 277
277
123
As coordenadas do centro e o raio das circunferências, cujas equações são
c1: (x – 5)2 + (y – 4)2 = 1 e c2: (x – 2)2 + y2 = 4, estão representadas na alternativa:
c1: Centro = (5, 4) e Raio =1 e c2: Centro = (2, 0 ) e Raio = 2
c1: Centro = (4, 5) e Raio =1 e c2: Centro = (2, 0 ) e Raio = 3
c1: Centro = (5, 0) e Raio = 2 e c2: Centro = (- 2, 4 ) e Raio =1
c1: Centro = (5, 4) e Raio = 1 e c2: Centro = (0, 2 ) e Raio = 2
c1: Centro = (5, - 4) e Raio = 2 e c2: Centro = (2, 0 ) e Raio = 2
Assinale a alternativa que representa a distância focal da hipérbole de equação 36x2 – 16y2 = 576.
R$ 120, 00
R$ 100, 00
R$ 80, 00
R$ 150, 00
R$ 60, 00
Reduzir a equação x2 + y2 + z2 – 25 = 0 à forma canônica e identificar a superfície.





Considerando a equação da superfície expressa por
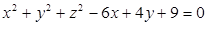
Assinale a alternativa correta.
Refere-se a uma superfície cilíndrica de centro de coordenadas (3, -2, 0) e raio igual a 4.
Refere-se a uma superfície cilíndrica de centro de coordenadas (3, 2, 0) e raio igual a 2.
Refere-se a uma superfície esférica de centro de coordenadas (3, 2, 0) e raio igual a 2.
Refere-se a uma superfície cônica de centro de coordenadas (-3, -2, 0) e raio igual a 4.
Refere-se a uma superfície esférica de centro de coordenadas (3, -2, 0) e raio igual a 2.
Dados os vetores u (-5,3,4) e v (2,1, 3). Assinale a alternativa que expressa o resultado do produto (3u + 2v) . (2u - v).
- 123
150
- 277
277
123
As coordenadas do centro e o raio das circunferências, cujas equações são
c1: (x – 5)2 + (y – 4)2 = 1 e c2: (x – 2)2 + y2 = 4, estão representadas na alternativa:
c1: Centro = (5, 4) e Raio =1 e c2: Centro = (2, 0 ) e Raio = 2
c1: Centro = (4, 5) e Raio =1 e c2: Centro = (2, 0 ) e Raio = 3
c1: Centro = (5, 0) e Raio = 2 e c2: Centro = (- 2, 4 ) e Raio =1
c1: Centro = (5, 4) e Raio = 1 e c2: Centro = (0, 2 ) e Raio = 2
c1: Centro = (5, - 4) e Raio = 2 e c2: Centro = (2, 0 ) e Raio = 2
Assinale a alternativa que representa a distância focal da hipérbole de equação 36x2 – 16y2 = 576.
Considerando a equação da superfície expressa por
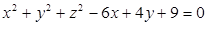
Assinale a alternativa correta.
Refere-se a uma superfície cilíndrica de centro de coordenadas (3, -2, 0) e raio igual a 4.
Refere-se a uma superfície cilíndrica de centro de coordenadas (3, 2, 0) e raio igual a 2.
Refere-se a uma superfície esférica de centro de coordenadas (3, 2, 0) e raio igual a 2.
Refere-se a uma superfície cônica de centro de coordenadas (-3, -2, 0) e raio igual a 4.
Refere-se a uma superfície esférica de centro de coordenadas (3, -2, 0) e raio igual a 2.
Dados os vetores u (-5,3,4) e v (2,1, 3). Assinale a alternativa que expressa o resultado do produto (3u + 2v) . (2u - v).
- 123
150
- 277
277
123
As coordenadas do centro e o raio das circunferências, cujas equações são
c1: (x – 5)2 + (y – 4)2 = 1 e c2: (x – 2)2 + y2 = 4, estão representadas na alternativa:
c1: Centro = (5, 4) e Raio =1 e c2: Centro = (2, 0 ) e Raio = 2
c1: Centro = (4, 5) e Raio =1 e c2: Centro = (2, 0 ) e Raio = 3
c1: Centro = (5, 0) e Raio = 2 e c2: Centro = (- 2, 4 ) e Raio =1
c1: Centro = (5, 4) e Raio = 1 e c2: Centro = (0, 2 ) e Raio = 2
c1: Centro = (5, - 4) e Raio = 2 e c2: Centro = (2, 0 ) e Raio = 2
Assinale a alternativa que representa a distância focal da hipérbole de equação 36x2 – 16y2 = 576.
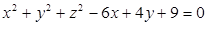
Refere-se a uma superfície cilíndrica de centro de coordenadas (3, -2, 0) e raio igual a 4.
Refere-se a uma superfície cilíndrica de centro de coordenadas (3, 2, 0) e raio igual a 2.
Refere-se a uma superfície esférica de centro de coordenadas (3, 2, 0) e raio igual a 2.
Refere-se a uma superfície cônica de centro de coordenadas (-3, -2, 0) e raio igual a 4.
Refere-se a uma superfície esférica de centro de coordenadas (3, -2, 0) e raio igual a 2.
Dados os vetores u (-5,3,4) e v (2,1, 3). Assinale a alternativa que expressa o resultado do produto (3u + 2v) . (2u - v).
- 123
150
- 277
277
123
As coordenadas do centro e o raio das circunferências, cujas equações são
c1: (x – 5)2 + (y – 4)2 = 1 e c2: (x – 2)2 + y2 = 4, estão representadas na alternativa:
c1: Centro = (5, 4) e Raio =1 e c2: Centro = (2, 0 ) e Raio = 2
c1: Centro = (4, 5) e Raio =1 e c2: Centro = (2, 0 ) e Raio = 3
c1: Centro = (5, 0) e Raio = 2 e c2: Centro = (- 2, 4 ) e Raio =1
c1: Centro = (5, 4) e Raio = 1 e c2: Centro = (0, 2 ) e Raio = 2
c1: Centro = (5, - 4) e Raio = 2 e c2: Centro = (2, 0 ) e Raio = 2
Assinale a alternativa que representa a distância focal da hipérbole de equação 36x2 – 16y2 = 576.
- 123
150
- 277
277
123
As coordenadas do centro e o raio das circunferências, cujas equações são
c1: (x – 5)2 + (y – 4)2 = 1 e c2: (x – 2)2 + y2 = 4, estão representadas na alternativa:
c1: Centro = (5, 4) e Raio =1 e c2: Centro = (2, 0 ) e Raio = 2
c1: Centro = (4, 5) e Raio =1 e c2: Centro = (2, 0 ) e Raio = 3
c1: Centro = (5, 0) e Raio = 2 e c2: Centro = (- 2, 4 ) e Raio =1
c1: Centro = (5, 4) e Raio = 1 e c2: Centro = (0, 2 ) e Raio = 2
c1: Centro = (5, - 4) e Raio = 2 e c2: Centro = (2, 0 ) e Raio = 2
Assinale a alternativa que representa a distância focal da hipérbole de equação 36x2 – 16y2 = 576.
c1: Centro = (5, 4) e Raio =1 e c2: Centro = (2, 0 ) e Raio = 2
c1: Centro = (4, 5) e Raio =1 e c2: Centro = (2, 0 ) e Raio = 3
c1: Centro = (5, 0) e Raio = 2 e c2: Centro = (- 2, 4 ) e Raio =1
c1: Centro = (5, 4) e Raio = 1 e c2: Centro = (0, 2 ) e Raio = 2
c1: Centro = (5, - 4) e Raio = 2 e c2: Centro = (2, 0 ) e Raio = 2