ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA
O sistema cartesiano apresentado a seguir é a representação matemática do mapa de uma cidade. Nele está traçado um paralelogramo ABCD, onde A, B, C e D representam pontos turísticos da cidade. O paralelogramo ABCD é o local onde estão localizados os hotéis dessa cidade.
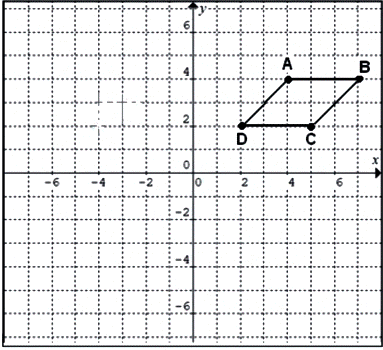
Em quais dos pontos do plano os hotéis dessa cidade estão localizados?
(4,4); (4,7); (2,5); (2,2)
(- 2,2); (- 5,2); (- 4,4); (- 7,4)
(- 2,- 2); (- 5,- 2); (- 4,- 4); (- 7,- 4)
(2, - 2); (5, - 2); (4, - 4); (7, - 4)
(4,4); (7,4); (5,2); (2,2)
Sistemas lineares é um conjunto de equações lineares, com m equações e n incógnitas. A solução de um sistema linear é a solução de todas as equações lineares.
A resolução de sistemas lineares tem aplicação nos mais diversos campos da ciência e da engenharia, como a eletrodinâmica, a eletrônica, a estática, a aerodinâmica, entre outras.
Sobre o sistema a seguir, é correto afirmar que:

x1 = 9/4
x1 = x2
x1 = - 4
x1 = - 1/3
x1 = - 3/4
A solução de um sistema linear é um conjunto de valores que satisfaz, ao mesmo tempo, todas as equações do sistema linear. A classificação é feita de acordo com a quantidade de soluções que ele admite:
- Sistema possível determinado (SPD): admite uma única solução;
- Sistema possível indeterminado (SPI): admite infinitas soluções;
- Sistema impossível (SI): não admite solução alguma.
Encontrando a solução do sistema linear a seguir, é correto o que se afirma em:

A terna ordenada (x, 2 x, 3) é a solução do sistema linear, classificado como sistema linear possível e indeterminado.
A terna ordenada (0, 2, 3) é a solução do sistema linear, classificado como sistema linear possível e determinado.
O sistema não possui solução, classificado como sistema linear impossível.
A terna ordenada (1, 2, 3) é a solução do sistema linear, classificado como sistema linear possível e determinado.
A terna ordenada (1, 2z, 3z) é a solução do sistema linear, classificado como sistema linear possível e indeterminado.


(4,4); (4,7); (2,5); (2,2)
(- 2,2); (- 5,2); (- 4,4); (- 7,4)
(- 2,- 2); (- 5,- 2); (- 4,- 4); (- 7,- 4)
(2, - 2); (5, - 2); (4, - 4); (7, - 4)
(4,4); (7,4); (5,2); (2,2)
Sistemas lineares é um conjunto de equações lineares, com m equações e n incógnitas. A solução de um sistema linear é a solução de todas as equações lineares.
A resolução de sistemas lineares tem aplicação nos mais diversos campos da ciência e da engenharia, como a eletrodinâmica, a eletrônica, a estática, a aerodinâmica, entre outras.
Sobre o sistema a seguir, é correto afirmar que:

x1 = 9/4
x1 = x2
x1 = - 4
x1 = - 1/3
x1 = - 3/4
A solução de um sistema linear é um conjunto de valores que satisfaz, ao mesmo tempo, todas as equações do sistema linear. A classificação é feita de acordo com a quantidade de soluções que ele admite:
- Sistema possível determinado (SPD): admite uma única solução;
- Sistema possível indeterminado (SPI): admite infinitas soluções;
- Sistema impossível (SI): não admite solução alguma.
Encontrando a solução do sistema linear a seguir, é correto o que se afirma em:

A terna ordenada (x, 2 x, 3) é a solução do sistema linear, classificado como sistema linear possível e indeterminado.
A terna ordenada (0, 2, 3) é a solução do sistema linear, classificado como sistema linear possível e determinado.
O sistema não possui solução, classificado como sistema linear impossível.
A terna ordenada (1, 2, 3) é a solução do sistema linear, classificado como sistema linear possível e determinado.
A terna ordenada (1, 2z, 3z) é a solução do sistema linear, classificado como sistema linear possível e indeterminado.

x1 = 9/4
x1 = x2
x1 = - 4
x1 = - 1/3
x1 = - 3/4
A solução de um sistema linear é um conjunto de valores que satisfaz, ao mesmo tempo, todas as equações do sistema linear. A classificação é feita de acordo com a quantidade de soluções que ele admite:
- Sistema possível determinado (SPD): admite uma única solução;
- Sistema possível indeterminado (SPI): admite infinitas soluções;
- Sistema impossível (SI): não admite solução alguma.
Encontrando a solução do sistema linear a seguir, é correto o que se afirma em:

A terna ordenada (x, 2 x, 3) é a solução do sistema linear, classificado como sistema linear possível e indeterminado.
A terna ordenada (0, 2, 3) é a solução do sistema linear, classificado como sistema linear possível e determinado.
O sistema não possui solução, classificado como sistema linear impossível.
A terna ordenada (1, 2, 3) é a solução do sistema linear, classificado como sistema linear possível e determinado.
A terna ordenada (1, 2z, 3z) é a solução do sistema linear, classificado como sistema linear possível e indeterminado.

A terna ordenada (x, 2 x, 3) é a solução do sistema linear, classificado como sistema linear possível e indeterminado.
A terna ordenada (0, 2, 3) é a solução do sistema linear, classificado como sistema linear possível e determinado.
O sistema não possui solução, classificado como sistema linear impossível.
A terna ordenada (1, 2, 3) é a solução do sistema linear, classificado como sistema linear possível e determinado.
A terna ordenada (1, 2z, 3z) é a solução do sistema linear, classificado como sistema linear possível e indeterminado.