TEORIA DAS ESTRUTURAS I
Qual o maior valor para cortante, em modulo, da estrutura abaixo?
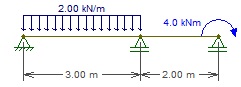
3,8 kN
4,3 kN
2,8 kN
3,2 kN
1,7 kN
A partir da estrutura abaixo, informar a quantidade total de reação de apoio, quantidade de equações de equilíbrio e a classificação da estrutura quanto ao equilíbrio estático.

6 reações de apoio, 3 equações de equilíbrio, hiperestática.
3 reações de apoio, 3 equações de equilíbrio, isostática.
6 reações de apoio, 5 equações de equilíbrio, hiperestática.
6 reações de apoio, 6 equações de equilíbrio, isostática.
6 reações de apoio, 5 equações de equilíbrio, hipostática.
Qual o valor do maior esforço cortante, em modulo, da estrutura representada na figura abaixo?
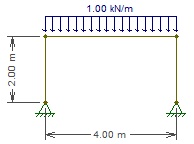
1,8 kN
1,5 kN
2,0 kN
0,8 kN
1,2 kN
Qual é o deslocamento horizontal do nó D do pórtico abaixo, desprezando-se as influências das deformações axiais e da força cortante? EI = 2.105 kNm² (constante).
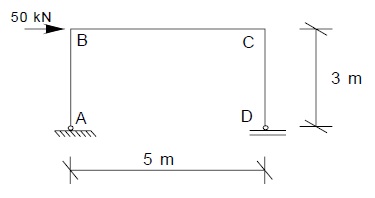
9.821 x 10-3 m para a esquerda
6,112 x 10-3 m para a direita
7,875 x 10-3 m para a esquerda
7,875 x 10-3 m para a direita
6,112 x 10-3 m para a esquerda
Com base na figura abaixo, calcule o cortante em B, utilizando as linhas de influências.

149,44kN.
69,44kN.
-410,56kN.
455,00kN.
-170,56kN.
Leia os itens abaixo:
I - O projeto de um elemento estrutural, como uma viga de ponte, envolve a determinação das posições das cargas que produzem valores extremos dos esforços nas seções do elemento.
II - Os esforços internos em alguns tipos de estruturas não variam apenas com a magnitude das cargas aplicadas, mas também com a posição de atuação das mesmas.
III - Pontes rodoviárias e ferroviárias ou pórticos industriais que suportam pontes rolantes para transporte de cargas.
Sobre as cargas móveis assinale a alternativa que indica qual dos itens acima está (ão) correto (os).
Todos os itens estão corretos
Somente II
Somente I e II
Somente I
Somente II e III
No caso de cargas móveis concentradas, para a obtenção de um determinado esforço numa certa seção, basta fazer o seguinte:
Dividir o valor da ordenada da linha de influência correspondente ao esforço desejado pela intensidade da carga concentrada.
Multiplicar o valor da ordenada da linha de influência correspondente ao esforço desejado pela intensidade da carga concentrada.
Multiplicar o valor da ordenada da linha de influência correspondente ao esforço desejado pela intensidade da carga distribuída.
Dividir o valor da ordenada da linha de influência correspondente ao esforço desejado pela intensidade da carga distribuída.
Fazer o somatório da ordenada da linha de influência correspondente ao esforço desejado e subtrair a intensidade da carga distribuída.
Analise o esquema abaixo:
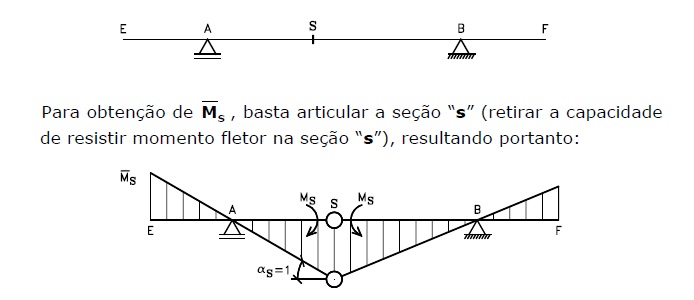
Para obtenção de QS, basta fazer o seguinte:
Determinar as reações na componente "X".
Calcular o cortante em A.
Liberar a translação vertical em “s” com o seguinte objetivo: retirar a capacidade de resistir à força cortante na seção “s”.
Fixar a translação vertical em “s” juntamente com o apoio fixo em A e B com o seguinte objetivo: aumentar a capacidade de resistir à força cortante na seção “s”.
Calcular o cortante em B.
As cargas podem ser classificadas em cargas permanentes e acidentais, assinale a alternativa correta que contém um exemplo de carga permanente.
Peso de neve acumulada em regiões frias
Ventos e empuxo da terra / água
Impactos laterais
Força centrífuga
Revestimento e materiais de enchimento
Com base na figura abaixo, calcule o momento fletor em B, utilizando as linhas de influências.


3,8 kN
4,3 kN
2,8 kN
3,2 kN
1,7 kN
A partir da estrutura abaixo, informar a quantidade total de reação de apoio, quantidade de equações de equilíbrio e a classificação da estrutura quanto ao equilíbrio estático.

6 reações de apoio, 3 equações de equilíbrio, hiperestática.
3 reações de apoio, 3 equações de equilíbrio, isostática.
6 reações de apoio, 5 equações de equilíbrio, hiperestática.
6 reações de apoio, 6 equações de equilíbrio, isostática.
6 reações de apoio, 5 equações de equilíbrio, hipostática.
Qual o valor do maior esforço cortante, em modulo, da estrutura representada na figura abaixo?

1,8 kN
1,5 kN
2,0 kN
0,8 kN
1,2 kN
Qual é o deslocamento horizontal do nó D do pórtico abaixo, desprezando-se as influências das deformações axiais e da força cortante? EI = 2.105 kNm² (constante).

9.821 x 10-3 m para a esquerda
6,112 x 10-3 m para a direita
7,875 x 10-3 m para a esquerda
7,875 x 10-3 m para a direita
6,112 x 10-3 m para a esquerda
Com base na figura abaixo, calcule o cortante em B, utilizando as linhas de influências.

149,44kN.
69,44kN.
-410,56kN.
455,00kN.
-170,56kN.
Leia os itens abaixo:
I - O projeto de um elemento estrutural, como uma viga de ponte, envolve a determinação das posições das cargas que produzem valores extremos dos esforços nas seções do elemento.
II - Os esforços internos em alguns tipos de estruturas não variam apenas com a magnitude das cargas aplicadas, mas também com a posição de atuação das mesmas.
III - Pontes rodoviárias e ferroviárias ou pórticos industriais que suportam pontes rolantes para transporte de cargas.
Sobre as cargas móveis assinale a alternativa que indica qual dos itens acima está (ão) correto (os).
Todos os itens estão corretos
Somente II
Somente I e II
Somente I
Somente II e III
No caso de cargas móveis concentradas, para a obtenção de um determinado esforço numa certa seção, basta fazer o seguinte:
Dividir o valor da ordenada da linha de influência correspondente ao esforço desejado pela intensidade da carga concentrada.
Multiplicar o valor da ordenada da linha de influência correspondente ao esforço desejado pela intensidade da carga concentrada.
Multiplicar o valor da ordenada da linha de influência correspondente ao esforço desejado pela intensidade da carga distribuída.
Dividir o valor da ordenada da linha de influência correspondente ao esforço desejado pela intensidade da carga distribuída.
Fazer o somatório da ordenada da linha de influência correspondente ao esforço desejado e subtrair a intensidade da carga distribuída.
Analise o esquema abaixo:

Para obtenção de QS, basta fazer o seguinte:
Determinar as reações na componente "X".
Calcular o cortante em A.
Liberar a translação vertical em “s” com o seguinte objetivo: retirar a capacidade de resistir à força cortante na seção “s”.
Fixar a translação vertical em “s” juntamente com o apoio fixo em A e B com o seguinte objetivo: aumentar a capacidade de resistir à força cortante na seção “s”.
Calcular o cortante em B.
As cargas podem ser classificadas em cargas permanentes e acidentais, assinale a alternativa correta que contém um exemplo de carga permanente.
Peso de neve acumulada em regiões frias
Ventos e empuxo da terra / água
Impactos laterais
Força centrífuga
Revestimento e materiais de enchimento
Com base na figura abaixo, calcule o momento fletor em B, utilizando as linhas de influências.


6 reações de apoio, 3 equações de equilíbrio, hiperestática.
3 reações de apoio, 3 equações de equilíbrio, isostática.
6 reações de apoio, 5 equações de equilíbrio, hiperestática.
6 reações de apoio, 6 equações de equilíbrio, isostática.
6 reações de apoio, 5 equações de equilíbrio, hipostática.
Qual o valor do maior esforço cortante, em modulo, da estrutura representada na figura abaixo?

1,8 kN
1,5 kN
2,0 kN
0,8 kN
1,2 kN
Qual é o deslocamento horizontal do nó D do pórtico abaixo, desprezando-se as influências das deformações axiais e da força cortante? EI = 2.105 kNm² (constante).

9.821 x 10-3 m para a esquerda
6,112 x 10-3 m para a direita
7,875 x 10-3 m para a esquerda
7,875 x 10-3 m para a direita
6,112 x 10-3 m para a esquerda
Com base na figura abaixo, calcule o cortante em B, utilizando as linhas de influências.

149,44kN.
69,44kN.
-410,56kN.
455,00kN.
-170,56kN.
Leia os itens abaixo:
I - O projeto de um elemento estrutural, como uma viga de ponte, envolve a determinação das posições das cargas que produzem valores extremos dos esforços nas seções do elemento.
II - Os esforços internos em alguns tipos de estruturas não variam apenas com a magnitude das cargas aplicadas, mas também com a posição de atuação das mesmas.
III - Pontes rodoviárias e ferroviárias ou pórticos industriais que suportam pontes rolantes para transporte de cargas.
Sobre as cargas móveis assinale a alternativa que indica qual dos itens acima está (ão) correto (os).
Todos os itens estão corretos
Somente II
Somente I e II
Somente I
Somente II e III
No caso de cargas móveis concentradas, para a obtenção de um determinado esforço numa certa seção, basta fazer o seguinte:
Dividir o valor da ordenada da linha de influência correspondente ao esforço desejado pela intensidade da carga concentrada.
Multiplicar o valor da ordenada da linha de influência correspondente ao esforço desejado pela intensidade da carga concentrada.
Multiplicar o valor da ordenada da linha de influência correspondente ao esforço desejado pela intensidade da carga distribuída.
Dividir o valor da ordenada da linha de influência correspondente ao esforço desejado pela intensidade da carga distribuída.
Fazer o somatório da ordenada da linha de influência correspondente ao esforço desejado e subtrair a intensidade da carga distribuída.
Analise o esquema abaixo:

Para obtenção de QS, basta fazer o seguinte:
Determinar as reações na componente "X".
Calcular o cortante em A.
Liberar a translação vertical em “s” com o seguinte objetivo: retirar a capacidade de resistir à força cortante na seção “s”.
Fixar a translação vertical em “s” juntamente com o apoio fixo em A e B com o seguinte objetivo: aumentar a capacidade de resistir à força cortante na seção “s”.
Calcular o cortante em B.
As cargas podem ser classificadas em cargas permanentes e acidentais, assinale a alternativa correta que contém um exemplo de carga permanente.
Peso de neve acumulada em regiões frias
Ventos e empuxo da terra / água
Impactos laterais
Força centrífuga
Revestimento e materiais de enchimento
Com base na figura abaixo, calcule o momento fletor em B, utilizando as linhas de influências.


1,8 kN
1,5 kN
2,0 kN
0,8 kN
1,2 kN
Qual é o deslocamento horizontal do nó D do pórtico abaixo, desprezando-se as influências das deformações axiais e da força cortante? EI = 2.105 kNm² (constante).

9.821 x 10-3 m para a esquerda
6,112 x 10-3 m para a direita
7,875 x 10-3 m para a esquerda
7,875 x 10-3 m para a direita
6,112 x 10-3 m para a esquerda
Com base na figura abaixo, calcule o cortante em B, utilizando as linhas de influências.

149,44kN.
69,44kN.
-410,56kN.
455,00kN.
-170,56kN.
Leia os itens abaixo:
I - O projeto de um elemento estrutural, como uma viga de ponte, envolve a determinação das posições das cargas que produzem valores extremos dos esforços nas seções do elemento.
II - Os esforços internos em alguns tipos de estruturas não variam apenas com a magnitude das cargas aplicadas, mas também com a posição de atuação das mesmas.
III - Pontes rodoviárias e ferroviárias ou pórticos industriais que suportam pontes rolantes para transporte de cargas.
Sobre as cargas móveis assinale a alternativa que indica qual dos itens acima está (ão) correto (os).
Todos os itens estão corretos
Somente II
Somente I e II
Somente I
Somente II e III
No caso de cargas móveis concentradas, para a obtenção de um determinado esforço numa certa seção, basta fazer o seguinte:
Dividir o valor da ordenada da linha de influência correspondente ao esforço desejado pela intensidade da carga concentrada.
Multiplicar o valor da ordenada da linha de influência correspondente ao esforço desejado pela intensidade da carga concentrada.
Multiplicar o valor da ordenada da linha de influência correspondente ao esforço desejado pela intensidade da carga distribuída.
Dividir o valor da ordenada da linha de influência correspondente ao esforço desejado pela intensidade da carga distribuída.
Fazer o somatório da ordenada da linha de influência correspondente ao esforço desejado e subtrair a intensidade da carga distribuída.
Analise o esquema abaixo:

Para obtenção de QS, basta fazer o seguinte:
Determinar as reações na componente "X".
Calcular o cortante em A.
Liberar a translação vertical em “s” com o seguinte objetivo: retirar a capacidade de resistir à força cortante na seção “s”.
Fixar a translação vertical em “s” juntamente com o apoio fixo em A e B com o seguinte objetivo: aumentar a capacidade de resistir à força cortante na seção “s”.
Calcular o cortante em B.
As cargas podem ser classificadas em cargas permanentes e acidentais, assinale a alternativa correta que contém um exemplo de carga permanente.
Peso de neve acumulada em regiões frias
Ventos e empuxo da terra / água
Impactos laterais
Força centrífuga
Revestimento e materiais de enchimento
Com base na figura abaixo, calcule o momento fletor em B, utilizando as linhas de influências.


9.821 x 10-3 m para a esquerda
6,112 x 10-3 m para a direita
7,875 x 10-3 m para a esquerda
7,875 x 10-3 m para a direita
6,112 x 10-3 m para a esquerda
Com base na figura abaixo, calcule o cortante em B, utilizando as linhas de influências.

149,44kN.
69,44kN.
-410,56kN.
455,00kN.
-170,56kN.
Leia os itens abaixo:
I - O projeto de um elemento estrutural, como uma viga de ponte, envolve a determinação das posições das cargas que produzem valores extremos dos esforços nas seções do elemento.
II - Os esforços internos em alguns tipos de estruturas não variam apenas com a magnitude das cargas aplicadas, mas também com a posição de atuação das mesmas.
III - Pontes rodoviárias e ferroviárias ou pórticos industriais que suportam pontes rolantes para transporte de cargas.
Sobre as cargas móveis assinale a alternativa que indica qual dos itens acima está (ão) correto (os).
Todos os itens estão corretos
Somente II
Somente I e II
Somente I
Somente II e III
No caso de cargas móveis concentradas, para a obtenção de um determinado esforço numa certa seção, basta fazer o seguinte:
Dividir o valor da ordenada da linha de influência correspondente ao esforço desejado pela intensidade da carga concentrada.
Multiplicar o valor da ordenada da linha de influência correspondente ao esforço desejado pela intensidade da carga concentrada.
Multiplicar o valor da ordenada da linha de influência correspondente ao esforço desejado pela intensidade da carga distribuída.
Dividir o valor da ordenada da linha de influência correspondente ao esforço desejado pela intensidade da carga distribuída.
Fazer o somatório da ordenada da linha de influência correspondente ao esforço desejado e subtrair a intensidade da carga distribuída.
Analise o esquema abaixo:

Para obtenção de QS, basta fazer o seguinte:
Determinar as reações na componente "X".
Calcular o cortante em A.
Liberar a translação vertical em “s” com o seguinte objetivo: retirar a capacidade de resistir à força cortante na seção “s”.
Fixar a translação vertical em “s” juntamente com o apoio fixo em A e B com o seguinte objetivo: aumentar a capacidade de resistir à força cortante na seção “s”.
Calcular o cortante em B.
As cargas podem ser classificadas em cargas permanentes e acidentais, assinale a alternativa correta que contém um exemplo de carga permanente.
Peso de neve acumulada em regiões frias
Ventos e empuxo da terra / água
Impactos laterais
Força centrífuga
Revestimento e materiais de enchimento
Com base na figura abaixo, calcule o momento fletor em B, utilizando as linhas de influências.

149,44kN.
69,44kN.
-410,56kN.
455,00kN.
-170,56kN.
Leia os itens abaixo:
I - O projeto de um elemento estrutural, como uma viga de ponte, envolve a determinação das posições das cargas que produzem valores extremos dos esforços nas seções do elemento.
II - Os esforços internos em alguns tipos de estruturas não variam apenas com a magnitude das cargas aplicadas, mas também com a posição de atuação das mesmas.
III - Pontes rodoviárias e ferroviárias ou pórticos industriais que suportam pontes rolantes para transporte de cargas.
Sobre as cargas móveis assinale a alternativa que indica qual dos itens acima está (ão) correto (os).
Todos os itens estão corretos
Somente II
Somente I e II
Somente I
Somente II e III
No caso de cargas móveis concentradas, para a obtenção de um determinado esforço numa certa seção, basta fazer o seguinte:
Dividir o valor da ordenada da linha de influência correspondente ao esforço desejado pela intensidade da carga concentrada.
Multiplicar o valor da ordenada da linha de influência correspondente ao esforço desejado pela intensidade da carga concentrada.
Multiplicar o valor da ordenada da linha de influência correspondente ao esforço desejado pela intensidade da carga distribuída.
Dividir o valor da ordenada da linha de influência correspondente ao esforço desejado pela intensidade da carga distribuída.
Fazer o somatório da ordenada da linha de influência correspondente ao esforço desejado e subtrair a intensidade da carga distribuída.
Analise o esquema abaixo:

Para obtenção de QS, basta fazer o seguinte:
Determinar as reações na componente "X".
Calcular o cortante em A.
Liberar a translação vertical em “s” com o seguinte objetivo: retirar a capacidade de resistir à força cortante na seção “s”.
Fixar a translação vertical em “s” juntamente com o apoio fixo em A e B com o seguinte objetivo: aumentar a capacidade de resistir à força cortante na seção “s”.
Calcular o cortante em B.
As cargas podem ser classificadas em cargas permanentes e acidentais, assinale a alternativa correta que contém um exemplo de carga permanente.
Peso de neve acumulada em regiões frias
Ventos e empuxo da terra / água
Impactos laterais
Força centrífuga
Revestimento e materiais de enchimento
Com base na figura abaixo, calcule o momento fletor em B, utilizando as linhas de influências.

Todos os itens estão corretos
Somente II
Somente I e II
Somente I
Somente II e III
No caso de cargas móveis concentradas, para a obtenção de um determinado esforço numa certa seção, basta fazer o seguinte:
Dividir o valor da ordenada da linha de influência correspondente ao esforço desejado pela intensidade da carga concentrada.
Multiplicar o valor da ordenada da linha de influência correspondente ao esforço desejado pela intensidade da carga concentrada.
Multiplicar o valor da ordenada da linha de influência correspondente ao esforço desejado pela intensidade da carga distribuída.
Dividir o valor da ordenada da linha de influência correspondente ao esforço desejado pela intensidade da carga distribuída.
Fazer o somatório da ordenada da linha de influência correspondente ao esforço desejado e subtrair a intensidade da carga distribuída.
Analise o esquema abaixo:

Para obtenção de QS, basta fazer o seguinte:
Determinar as reações na componente "X".
Calcular o cortante em A.
Liberar a translação vertical em “s” com o seguinte objetivo: retirar a capacidade de resistir à força cortante na seção “s”.
Fixar a translação vertical em “s” juntamente com o apoio fixo em A e B com o seguinte objetivo: aumentar a capacidade de resistir à força cortante na seção “s”.
Calcular o cortante em B.
As cargas podem ser classificadas em cargas permanentes e acidentais, assinale a alternativa correta que contém um exemplo de carga permanente.
Peso de neve acumulada em regiões frias
Ventos e empuxo da terra / água
Impactos laterais
Força centrífuga
Revestimento e materiais de enchimento
Com base na figura abaixo, calcule o momento fletor em B, utilizando as linhas de influências.

Dividir o valor da ordenada da linha de influência correspondente ao esforço desejado pela intensidade da carga concentrada.
Multiplicar o valor da ordenada da linha de influência correspondente ao esforço desejado pela intensidade da carga concentrada.
Multiplicar o valor da ordenada da linha de influência correspondente ao esforço desejado pela intensidade da carga distribuída.
Dividir o valor da ordenada da linha de influência correspondente ao esforço desejado pela intensidade da carga distribuída.
Fazer o somatório da ordenada da linha de influência correspondente ao esforço desejado e subtrair a intensidade da carga distribuída.
Analise o esquema abaixo:

Para obtenção de QS, basta fazer o seguinte:
Determinar as reações na componente "X".
Calcular o cortante em A.
Liberar a translação vertical em “s” com o seguinte objetivo: retirar a capacidade de resistir à força cortante na seção “s”.
Fixar a translação vertical em “s” juntamente com o apoio fixo em A e B com o seguinte objetivo: aumentar a capacidade de resistir à força cortante na seção “s”.
Calcular o cortante em B.
As cargas podem ser classificadas em cargas permanentes e acidentais, assinale a alternativa correta que contém um exemplo de carga permanente.
Peso de neve acumulada em regiões frias
Ventos e empuxo da terra / água
Impactos laterais
Força centrífuga
Revestimento e materiais de enchimento
Com base na figura abaixo, calcule o momento fletor em B, utilizando as linhas de influências.


Determinar as reações na componente "X".
Calcular o cortante em A.
Liberar a translação vertical em “s” com o seguinte objetivo: retirar a capacidade de resistir à força cortante na seção “s”.
Fixar a translação vertical em “s” juntamente com o apoio fixo em A e B com o seguinte objetivo: aumentar a capacidade de resistir à força cortante na seção “s”.
Calcular o cortante em B.
As cargas podem ser classificadas em cargas permanentes e acidentais, assinale a alternativa correta que contém um exemplo de carga permanente.
Peso de neve acumulada em regiões frias
Ventos e empuxo da terra / água
Impactos laterais
Força centrífuga
Revestimento e materiais de enchimento
Com base na figura abaixo, calcule o momento fletor em B, utilizando as linhas de influências.

Peso de neve acumulada em regiões frias
Ventos e empuxo da terra / água
Impactos laterais
Força centrífuga
Revestimento e materiais de enchimento