TEORIA DAS ESTRUTURAS I
Nas edificações, existem várias forças (cargas) atuando sobre ela, o peso próprio dos pilares, vigas e lajes; o peso próprio das paredes, dos revestimentos de piso, dos forros e das coberturas. Qual é o nome deste tipo de carga atuante?
Carga permanente
Carga virtual
Carga oblíqua
Carga direcional
Carga de momento
No caso de cargas móveis uniformemente distribuídas, para a obtenção de um determinado esforço numa certa seção, devemos fazer o seguinte:
Multiplicar o valor da área da projeção do carregamento distribuído da linha de influência correspondente ao esforço desejado pela intensidade da carga uniforme.
Dividir o valor da área da projeção do carregamento distribuído da linha de influência correspondente ao esforço desejado pela intensidade da carga uniforme.
Dividir o valor da área da projeção do carregamento concentrado da linha de influência correspondente ao esforço desejado pela intensidade da carga residual.
Multiplicar o valor da área da projeção do carregamento concentrado da linha de influência correspondente ao esforço desejado pela intensidade da carga residual.
Somar o valor da área da projeção do carregamento concentrado da linha de influência correspondente ao esforço desejado pela intensidade da carga residual subtraída da distribuição de cargas.
Os corpos elásticos são os corpos:
Colunas transversas
Deformáveis
Vigas sobrepostas
Vigas transversais
Estruturais
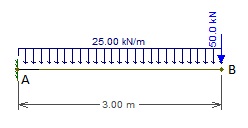
Qual é a rotação do ponto B, desprezando-se o efeito das deformações devidas à força cortante? EI = 2.105 kNm²
1,688 . 10-3 rad
2,437 . 10-3 rad
3,526 . 10-3 rad
4,065 . 10-3 rad
1,836 . 10-3 rad
Toda estrutura que é submetida a uma situação de cargas móveis, são submetidos a situações de envoltórias. Sendo assim, podemos definir que as ENVOLTÓRIAS que calculamos para situações de estruturas submetidas a cargas móveis são:
A representação gráfica da soma dos diagramas de extremos com os diagramas de esforços internos de uma estrutura.
A representação gráfica da soma dos diagramas internos com os diagramas de esforços externos de uma estrutura.
As regiões limite de máximo momento fletor e esforço cortante de um trem-tipo sobre uma estrutura qualquer, independentemente das demais cargas permanentes aplicadas, consideradas posteriormente.
As regiões limite de mínimo momento fletor e esforço cortante de um trem-tipo sobre uma estrutura qualquer, independentemente das demais cargas permanentes aplicadas, consideradas posteriormente.
A representação gráfica de uma faixa de trabalho dos mínimos e máximos esforços originados a partir da soma dos carregamentos permanentes e das cargas móveis, necessária ao dimensionamento de estruturas.
Considerando ainda as situações de cargas móveis que são submetidas a situações de envoltórias, existem cálculos que fazem-se necessários:
I. Elaborar uma tabela somando os valores extremos devido às forças móveis e os valores devidos ao carregamento permanente;
II. Dividir a estrutura em diferentes seções transversais;
III. Traçar as linhas das envoltórias;
IV. Determinar as linhas de influência dos esforços devidas ao trem-tipo nas posições críticas.
Pode-se dizer que, a sequência correta dos passos para a resolução do problema está em:
IV, III, I, II.
II, IV, III, I.
III,II, IV, I.
IV, II, I, III.
II, IV, I, III.
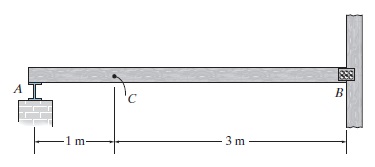
A viga suporta uma carga permanente e uniformemente distribuida de 500 N/m(já inclusos o peso próprio da estrutura) que atuará ao londo de toda a estrutura e uma carga móvel concentrada única de 3.000 N.
Determine:
- O momento máximo positivo em C;
- o cortante máximo positivo em C.
Nota: suponha que apoio em A seja um rolo e B um pino.
M = 789 kN.m, V = 875 kN
M = 3 kN.m, V = 2,75 kN
M = 8 kN.m, V = 25 kN
M = 150 kN.m, V = 200 kN
M = 0,25 kN.m, V = 1,45 kN
Considere o quadro isostático a seguir para responder

O maior valor do momento fletor no trecho 3-4, em kN.m, é
90,00
920,00
500,00
1170,00
Zero
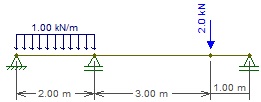
Quais os maiores momentos máximos, (positivo e negativo) nesta sequencia e em modulo, devido ao carregamento da estrutura abaixo?
1,3 kNm e 0,2 kNm
0,2 kNm e 0,8 kNm
0,2 kNm e 1,3 kNm
0,8 kNm e 0,8 kNm
1,3 kNm e 0,8 kNm
Quais os momentos máximos (positivo e negativo), em modulo e nesta sequencia, devido ao carregamento da estrutura abaixo?

Carga permanente
Carga virtual
Carga oblíqua
Carga direcional
Carga de momento
No caso de cargas móveis uniformemente distribuídas, para a obtenção de um determinado esforço numa certa seção, devemos fazer o seguinte:
Multiplicar o valor da área da projeção do carregamento distribuído da linha de influência correspondente ao esforço desejado pela intensidade da carga uniforme.
Dividir o valor da área da projeção do carregamento distribuído da linha de influência correspondente ao esforço desejado pela intensidade da carga uniforme.
Dividir o valor da área da projeção do carregamento concentrado da linha de influência correspondente ao esforço desejado pela intensidade da carga residual.
Multiplicar o valor da área da projeção do carregamento concentrado da linha de influência correspondente ao esforço desejado pela intensidade da carga residual.
Somar o valor da área da projeção do carregamento concentrado da linha de influência correspondente ao esforço desejado pela intensidade da carga residual subtraída da distribuição de cargas.
Os corpos elásticos são os corpos:
Colunas transversas
Deformáveis
Vigas sobrepostas
Vigas transversais
Estruturais
Qual é a rotação do ponto B, desprezando-se o efeito das deformações devidas à força cortante? EI = 2.105 kNm²

1,688 . 10-3 rad
2,437 . 10-3 rad
3,526 . 10-3 rad
4,065 . 10-3 rad
1,836 . 10-3 rad
Toda estrutura que é submetida a uma situação de cargas móveis, são submetidos a situações de envoltórias. Sendo assim, podemos definir que as ENVOLTÓRIAS que calculamos para situações de estruturas submetidas a cargas móveis são:
A representação gráfica da soma dos diagramas de extremos com os diagramas de esforços internos de uma estrutura.
A representação gráfica da soma dos diagramas internos com os diagramas de esforços externos de uma estrutura.
As regiões limite de máximo momento fletor e esforço cortante de um trem-tipo sobre uma estrutura qualquer, independentemente das demais cargas permanentes aplicadas, consideradas posteriormente.
As regiões limite de mínimo momento fletor e esforço cortante de um trem-tipo sobre uma estrutura qualquer, independentemente das demais cargas permanentes aplicadas, consideradas posteriormente.
A representação gráfica de uma faixa de trabalho dos mínimos e máximos esforços originados a partir da soma dos carregamentos permanentes e das cargas móveis, necessária ao dimensionamento de estruturas.
Considerando ainda as situações de cargas móveis que são submetidas a situações de envoltórias, existem cálculos que fazem-se necessários:
I. Elaborar uma tabela somando os valores extremos devido às forças móveis e os valores devidos ao carregamento permanente;
II. Dividir a estrutura em diferentes seções transversais;
III. Traçar as linhas das envoltórias;
IV. Determinar as linhas de influência dos esforços devidas ao trem-tipo nas posições críticas.
Pode-se dizer que, a sequência correta dos passos para a resolução do problema está em:
IV, III, I, II.
II, IV, III, I.
III,II, IV, I.
IV, II, I, III.
II, IV, I, III.
A viga suporta uma carga permanente e uniformemente distribuida de 500 N/m(já inclusos o peso próprio da estrutura) que atuará ao londo de toda a estrutura e uma carga móvel concentrada única de 3.000 N.
Determine:
- O momento máximo positivo em C;
- o cortante máximo positivo em C.
Nota: suponha que apoio em A seja um rolo e B um pino.

M = 789 kN.m, V = 875 kN
M = 3 kN.m, V = 2,75 kN
M = 8 kN.m, V = 25 kN
M = 150 kN.m, V = 200 kN
M = 0,25 kN.m, V = 1,45 kN
Considere o quadro isostático a seguir para responder

O maior valor do momento fletor no trecho 3-4, em kN.m, é
90,00
920,00
500,00
1170,00
Zero
Quais os maiores momentos máximos, (positivo e negativo) nesta sequencia e em modulo, devido ao carregamento da estrutura abaixo?

1,3 kNm e 0,2 kNm
0,2 kNm e 0,8 kNm
0,2 kNm e 1,3 kNm
0,8 kNm e 0,8 kNm
1,3 kNm e 0,8 kNm
Quais os momentos máximos (positivo e negativo), em modulo e nesta sequencia, devido ao carregamento da estrutura abaixo?

Multiplicar o valor da área da projeção do carregamento distribuído da linha de influência correspondente ao esforço desejado pela intensidade da carga uniforme.
Dividir o valor da área da projeção do carregamento distribuído da linha de influência correspondente ao esforço desejado pela intensidade da carga uniforme.
Dividir o valor da área da projeção do carregamento concentrado da linha de influência correspondente ao esforço desejado pela intensidade da carga residual.
Multiplicar o valor da área da projeção do carregamento concentrado da linha de influência correspondente ao esforço desejado pela intensidade da carga residual.
Somar o valor da área da projeção do carregamento concentrado da linha de influência correspondente ao esforço desejado pela intensidade da carga residual subtraída da distribuição de cargas.
Os corpos elásticos são os corpos:
Colunas transversas
Deformáveis
Vigas sobrepostas
Vigas transversais
Estruturais
Qual é a rotação do ponto B, desprezando-se o efeito das deformações devidas à força cortante? EI = 2.105 kNm²

1,688 . 10-3 rad
2,437 . 10-3 rad
3,526 . 10-3 rad
4,065 . 10-3 rad
1,836 . 10-3 rad
Toda estrutura que é submetida a uma situação de cargas móveis, são submetidos a situações de envoltórias. Sendo assim, podemos definir que as ENVOLTÓRIAS que calculamos para situações de estruturas submetidas a cargas móveis são:
A representação gráfica da soma dos diagramas de extremos com os diagramas de esforços internos de uma estrutura.
A representação gráfica da soma dos diagramas internos com os diagramas de esforços externos de uma estrutura.
As regiões limite de máximo momento fletor e esforço cortante de um trem-tipo sobre uma estrutura qualquer, independentemente das demais cargas permanentes aplicadas, consideradas posteriormente.
As regiões limite de mínimo momento fletor e esforço cortante de um trem-tipo sobre uma estrutura qualquer, independentemente das demais cargas permanentes aplicadas, consideradas posteriormente.
A representação gráfica de uma faixa de trabalho dos mínimos e máximos esforços originados a partir da soma dos carregamentos permanentes e das cargas móveis, necessária ao dimensionamento de estruturas.
Considerando ainda as situações de cargas móveis que são submetidas a situações de envoltórias, existem cálculos que fazem-se necessários:
I. Elaborar uma tabela somando os valores extremos devido às forças móveis e os valores devidos ao carregamento permanente;
II. Dividir a estrutura em diferentes seções transversais;
III. Traçar as linhas das envoltórias;
IV. Determinar as linhas de influência dos esforços devidas ao trem-tipo nas posições críticas.
Pode-se dizer que, a sequência correta dos passos para a resolução do problema está em:
IV, III, I, II.
II, IV, III, I.
III,II, IV, I.
IV, II, I, III.
II, IV, I, III.
A viga suporta uma carga permanente e uniformemente distribuida de 500 N/m(já inclusos o peso próprio da estrutura) que atuará ao londo de toda a estrutura e uma carga móvel concentrada única de 3.000 N.
Determine:
- O momento máximo positivo em C;
- o cortante máximo positivo em C.
Nota: suponha que apoio em A seja um rolo e B um pino.

M = 789 kN.m, V = 875 kN
M = 3 kN.m, V = 2,75 kN
M = 8 kN.m, V = 25 kN
M = 150 kN.m, V = 200 kN
M = 0,25 kN.m, V = 1,45 kN
Considere o quadro isostático a seguir para responder

O maior valor do momento fletor no trecho 3-4, em kN.m, é
90,00
920,00
500,00
1170,00
Zero
Quais os maiores momentos máximos, (positivo e negativo) nesta sequencia e em modulo, devido ao carregamento da estrutura abaixo?

1,3 kNm e 0,2 kNm
0,2 kNm e 0,8 kNm
0,2 kNm e 1,3 kNm
0,8 kNm e 0,8 kNm
1,3 kNm e 0,8 kNm
Quais os momentos máximos (positivo e negativo), em modulo e nesta sequencia, devido ao carregamento da estrutura abaixo?

Colunas transversas
Deformáveis
Vigas sobrepostas
Vigas transversais
Estruturais
Qual é a rotação do ponto B, desprezando-se o efeito das deformações devidas à força cortante? EI = 2.105 kNm²

1,688 . 10-3 rad
2,437 . 10-3 rad
3,526 . 10-3 rad
4,065 . 10-3 rad
1,836 . 10-3 rad
Toda estrutura que é submetida a uma situação de cargas móveis, são submetidos a situações de envoltórias. Sendo assim, podemos definir que as ENVOLTÓRIAS que calculamos para situações de estruturas submetidas a cargas móveis são:
A representação gráfica da soma dos diagramas de extremos com os diagramas de esforços internos de uma estrutura.
A representação gráfica da soma dos diagramas internos com os diagramas de esforços externos de uma estrutura.
As regiões limite de máximo momento fletor e esforço cortante de um trem-tipo sobre uma estrutura qualquer, independentemente das demais cargas permanentes aplicadas, consideradas posteriormente.
As regiões limite de mínimo momento fletor e esforço cortante de um trem-tipo sobre uma estrutura qualquer, independentemente das demais cargas permanentes aplicadas, consideradas posteriormente.
A representação gráfica de uma faixa de trabalho dos mínimos e máximos esforços originados a partir da soma dos carregamentos permanentes e das cargas móveis, necessária ao dimensionamento de estruturas.
Considerando ainda as situações de cargas móveis que são submetidas a situações de envoltórias, existem cálculos que fazem-se necessários:
I. Elaborar uma tabela somando os valores extremos devido às forças móveis e os valores devidos ao carregamento permanente;
II. Dividir a estrutura em diferentes seções transversais;
III. Traçar as linhas das envoltórias;
IV. Determinar as linhas de influência dos esforços devidas ao trem-tipo nas posições críticas.
Pode-se dizer que, a sequência correta dos passos para a resolução do problema está em:
IV, III, I, II.
II, IV, III, I.
III,II, IV, I.
IV, II, I, III.
II, IV, I, III.
A viga suporta uma carga permanente e uniformemente distribuida de 500 N/m(já inclusos o peso próprio da estrutura) que atuará ao londo de toda a estrutura e uma carga móvel concentrada única de 3.000 N.
Determine:
- O momento máximo positivo em C;
- o cortante máximo positivo em C.
Nota: suponha que apoio em A seja um rolo e B um pino.

M = 789 kN.m, V = 875 kN
M = 3 kN.m, V = 2,75 kN
M = 8 kN.m, V = 25 kN
M = 150 kN.m, V = 200 kN
M = 0,25 kN.m, V = 1,45 kN
Considere o quadro isostático a seguir para responder

O maior valor do momento fletor no trecho 3-4, em kN.m, é
90,00
920,00
500,00
1170,00
Zero
Quais os maiores momentos máximos, (positivo e negativo) nesta sequencia e em modulo, devido ao carregamento da estrutura abaixo?

1,3 kNm e 0,2 kNm
0,2 kNm e 0,8 kNm
0,2 kNm e 1,3 kNm
0,8 kNm e 0,8 kNm
1,3 kNm e 0,8 kNm
Quais os momentos máximos (positivo e negativo), em modulo e nesta sequencia, devido ao carregamento da estrutura abaixo?


1,688 . 10-3 rad
2,437 . 10-3 rad
3,526 . 10-3 rad
4,065 . 10-3 rad
1,836 . 10-3 rad
Toda estrutura que é submetida a uma situação de cargas móveis, são submetidos a situações de envoltórias. Sendo assim, podemos definir que as ENVOLTÓRIAS que calculamos para situações de estruturas submetidas a cargas móveis são:
A representação gráfica da soma dos diagramas de extremos com os diagramas de esforços internos de uma estrutura.
A representação gráfica da soma dos diagramas internos com os diagramas de esforços externos de uma estrutura.
As regiões limite de máximo momento fletor e esforço cortante de um trem-tipo sobre uma estrutura qualquer, independentemente das demais cargas permanentes aplicadas, consideradas posteriormente.
As regiões limite de mínimo momento fletor e esforço cortante de um trem-tipo sobre uma estrutura qualquer, independentemente das demais cargas permanentes aplicadas, consideradas posteriormente.
A representação gráfica de uma faixa de trabalho dos mínimos e máximos esforços originados a partir da soma dos carregamentos permanentes e das cargas móveis, necessária ao dimensionamento de estruturas.
Considerando ainda as situações de cargas móveis que são submetidas a situações de envoltórias, existem cálculos que fazem-se necessários:
I. Elaborar uma tabela somando os valores extremos devido às forças móveis e os valores devidos ao carregamento permanente;
II. Dividir a estrutura em diferentes seções transversais;
III. Traçar as linhas das envoltórias;
IV. Determinar as linhas de influência dos esforços devidas ao trem-tipo nas posições críticas.
Pode-se dizer que, a sequência correta dos passos para a resolução do problema está em:
IV, III, I, II.
II, IV, III, I.
III,II, IV, I.
IV, II, I, III.
II, IV, I, III.
A viga suporta uma carga permanente e uniformemente distribuida de 500 N/m(já inclusos o peso próprio da estrutura) que atuará ao londo de toda a estrutura e uma carga móvel concentrada única de 3.000 N.
Determine:
- O momento máximo positivo em C;
- o cortante máximo positivo em C.
Nota: suponha que apoio em A seja um rolo e B um pino.

M = 789 kN.m, V = 875 kN
M = 3 kN.m, V = 2,75 kN
M = 8 kN.m, V = 25 kN
M = 150 kN.m, V = 200 kN
M = 0,25 kN.m, V = 1,45 kN
Considere o quadro isostático a seguir para responder

O maior valor do momento fletor no trecho 3-4, em kN.m, é
90,00
920,00
500,00
1170,00
Zero
Quais os maiores momentos máximos, (positivo e negativo) nesta sequencia e em modulo, devido ao carregamento da estrutura abaixo?

1,3 kNm e 0,2 kNm
0,2 kNm e 0,8 kNm
0,2 kNm e 1,3 kNm
0,8 kNm e 0,8 kNm
1,3 kNm e 0,8 kNm
Quais os momentos máximos (positivo e negativo), em modulo e nesta sequencia, devido ao carregamento da estrutura abaixo?

A representação gráfica da soma dos diagramas de extremos com os diagramas de esforços internos de uma estrutura.
A representação gráfica da soma dos diagramas internos com os diagramas de esforços externos de uma estrutura.
As regiões limite de máximo momento fletor e esforço cortante de um trem-tipo sobre uma estrutura qualquer, independentemente das demais cargas permanentes aplicadas, consideradas posteriormente.
As regiões limite de mínimo momento fletor e esforço cortante de um trem-tipo sobre uma estrutura qualquer, independentemente das demais cargas permanentes aplicadas, consideradas posteriormente.
A representação gráfica de uma faixa de trabalho dos mínimos e máximos esforços originados a partir da soma dos carregamentos permanentes e das cargas móveis, necessária ao dimensionamento de estruturas.
Considerando ainda as situações de cargas móveis que são submetidas a situações de envoltórias, existem cálculos que fazem-se necessários:
I. Elaborar uma tabela somando os valores extremos devido às forças móveis e os valores devidos ao carregamento permanente;
II. Dividir a estrutura em diferentes seções transversais;
III. Traçar as linhas das envoltórias;
IV. Determinar as linhas de influência dos esforços devidas ao trem-tipo nas posições críticas.
Pode-se dizer que, a sequência correta dos passos para a resolução do problema está em:
IV, III, I, II.
II, IV, III, I.
III,II, IV, I.
IV, II, I, III.
II, IV, I, III.
A viga suporta uma carga permanente e uniformemente distribuida de 500 N/m(já inclusos o peso próprio da estrutura) que atuará ao londo de toda a estrutura e uma carga móvel concentrada única de 3.000 N.
Determine:
- O momento máximo positivo em C;
- o cortante máximo positivo em C.
Nota: suponha que apoio em A seja um rolo e B um pino.

M = 789 kN.m, V = 875 kN
M = 3 kN.m, V = 2,75 kN
M = 8 kN.m, V = 25 kN
M = 150 kN.m, V = 200 kN
M = 0,25 kN.m, V = 1,45 kN
Considere o quadro isostático a seguir para responder

O maior valor do momento fletor no trecho 3-4, em kN.m, é
90,00
920,00
500,00
1170,00
Zero
Quais os maiores momentos máximos, (positivo e negativo) nesta sequencia e em modulo, devido ao carregamento da estrutura abaixo?

1,3 kNm e 0,2 kNm
0,2 kNm e 0,8 kNm
0,2 kNm e 1,3 kNm
0,8 kNm e 0,8 kNm
1,3 kNm e 0,8 kNm
Quais os momentos máximos (positivo e negativo), em modulo e nesta sequencia, devido ao carregamento da estrutura abaixo?

IV, III, I, II.
II, IV, III, I.
III,II, IV, I.
IV, II, I, III.
II, IV, I, III.
A viga suporta uma carga permanente e uniformemente distribuida de 500 N/m(já inclusos o peso próprio da estrutura) que atuará ao londo de toda a estrutura e uma carga móvel concentrada única de 3.000 N.
Determine:
- O momento máximo positivo em C;
- o cortante máximo positivo em C.
Nota: suponha que apoio em A seja um rolo e B um pino.

M = 789 kN.m, V = 875 kN
M = 3 kN.m, V = 2,75 kN
M = 8 kN.m, V = 25 kN
M = 150 kN.m, V = 200 kN
M = 0,25 kN.m, V = 1,45 kN
Considere o quadro isostático a seguir para responder

O maior valor do momento fletor no trecho 3-4, em kN.m, é
90,00
920,00
500,00
1170,00
Zero
Quais os maiores momentos máximos, (positivo e negativo) nesta sequencia e em modulo, devido ao carregamento da estrutura abaixo?

1,3 kNm e 0,2 kNm
0,2 kNm e 0,8 kNm
0,2 kNm e 1,3 kNm
0,8 kNm e 0,8 kNm
1,3 kNm e 0,8 kNm
Quais os momentos máximos (positivo e negativo), em modulo e nesta sequencia, devido ao carregamento da estrutura abaixo?


M = 789 kN.m, V = 875 kN
M = 3 kN.m, V = 2,75 kN
M = 8 kN.m, V = 25 kN
M = 150 kN.m, V = 200 kN
M = 0,25 kN.m, V = 1,45 kN
Considere o quadro isostático a seguir para responder

O maior valor do momento fletor no trecho 3-4, em kN.m, é
90,00
920,00
500,00
1170,00
Zero
Quais os maiores momentos máximos, (positivo e negativo) nesta sequencia e em modulo, devido ao carregamento da estrutura abaixo?

1,3 kNm e 0,2 kNm
0,2 kNm e 0,8 kNm
0,2 kNm e 1,3 kNm
0,8 kNm e 0,8 kNm
1,3 kNm e 0,8 kNm
Quais os momentos máximos (positivo e negativo), em modulo e nesta sequencia, devido ao carregamento da estrutura abaixo?

90,00
920,00
500,00
1170,00
Zero
Quais os maiores momentos máximos, (positivo e negativo) nesta sequencia e em modulo, devido ao carregamento da estrutura abaixo?

1,3 kNm e 0,2 kNm
0,2 kNm e 0,8 kNm
0,2 kNm e 1,3 kNm
0,8 kNm e 0,8 kNm
1,3 kNm e 0,8 kNm
Quais os momentos máximos (positivo e negativo), em modulo e nesta sequencia, devido ao carregamento da estrutura abaixo?


1,3 kNm e 0,2 kNm
0,2 kNm e 0,8 kNm
0,2 kNm e 1,3 kNm
0,8 kNm e 0,8 kNm
1,3 kNm e 0,8 kNm
Quais os momentos máximos (positivo e negativo), em modulo e nesta sequencia, devido ao carregamento da estrutura abaixo?

